The zirconium dioxide O2 sensor working principle measures partial pressure of oxygen in a mixture of gases. This typically causes confusion amongst PST’s customers as most oxygen sensors on the market measure oxygen concentration.
But, what is partial pressure? It is a question we are asked frequently when it comes to the O2 sensor working principle. In this article, we will address the definition of partial pressure, the physics behind it, how you calculate partial pressure and how to convert the oxygen partial pressure into volumetric content for those interested in oxygen concentration.
Partial Pressure: The Definition
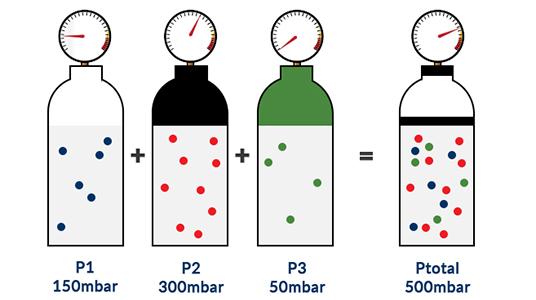
The partial pressure is defined as the pressure of a single gas component in a mixture of gases. It corresponds to the total pressure which the single gas component would exert if it alone occupied the whole volume.
Daltons Law: The Physics
The theory of the o2 sensor working principle is detailed here. The total pressure (Ptotal) of a mixture of ideal gases is equal to the sum of the partial pressures (Pi) of the individual gases in that mixture.
| k |
| i=1 |
| ni |
| ntotal |
| Pi |
| Ptotal |
| ni | Number of particles in gas |
| ntotal | Total number of particles |
| pi | Partial pressure of gas i |
| Ptotal | Total pressure |
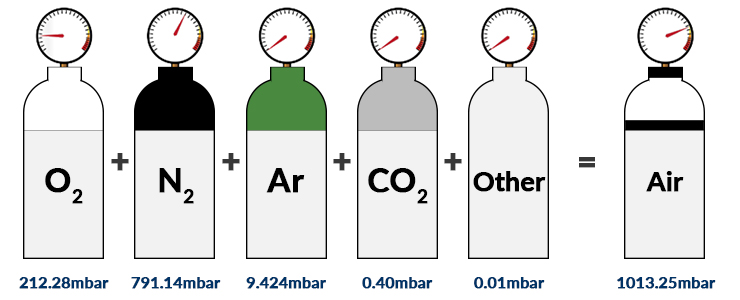
Example 1:
The atmospheric pressure at sea level (under standard atmospheric conditions) is 1013.25mbar. Here, the main components of dry air are nitrogen (78.08% Vol.), oxygen (20.95% Vol.), argon (0.93% Vol.) and carbon dioxide (0.040% Vol.). The volumetric content (%) can be equated to the number of particles (n) since the above gases can be approximated as ideal gases.
Equation 2 can be solved for the partial pressure of an individual gas (i) to get:
| ni |
| ntotal |
| 20.95% |
| 100% |
Of course, this value is only relevant when the atmosphere is dry (0% humidity). If moisture is present a proportion of the total pressure is taken up by water vapour pressure. Therefore, the partial oxygen pressure (ppO₂) can be calculated more accurately when relative humidity and ambient temperature are measured along with the total barometric pressure.
Firstly, water vapour pressure is calculated:
| HRel |
| 100 |
| WVP | Water Vapour Pressure (mbar) |
| HRel | Relative Humidity (%) |
| WVPmax | Maximum Water Vapour Pressure (mbar) |
For a known ambient temperature, maximum water vapour pressure (WVPmax) can be determined from the lookup table below. The maximum water vapour pressure is also referred to as the dew point. Warmer air can hold more water vapour and so has a higher WVPmax.
| Temperature (°C) | Max water vapour pressure (mbar) | Temperature (°C) | Max water vapour pressure (mbar) |
| 0 | 6.1 | 31 | 44.92 |
| 1 | 6.57 | 32 | 47.54 |
| 2 | 7.06 | 33 | 50.3 |
| 3 | 7.58 | 34 | 53.19 |
| 4 | 8.13 | 35 | 56.23 |
| 5 | 8.72 | 36 | 59.42 |
| 6 | 9.35 | 37 | 62.76 |
| 7 | 10.01 | 38 | 66.27 |
| 8 | 10.72 | 39 | 69.93 |
| 9 | 11.47 | 40 | 73.77 |
| 10 | 12.27 | 42.5 | 84.19 |
| 11 | 13.12 | 45 | 95.85 |
| 12 | 14.02 | 47.5 | 108.86 |
| 13 | 14.97 | 50 | 123.86 |
| 14 | 15.98 | 52.5 | 139.5 |
| 15 | 17.04 | 55 | 457.42 |
| 16 | 18.17 | 57.5 | 177.25 |
| 17 | 19.37 | 60 | 199.17 |
| 18 | 20.63 | 62.5 | 223.36 |
| 19 | 21.96 | 65 | 250.01 |
| 20 | 23.37 | 67.5 | 279.31 |
| 21 | 24.86 | 70 | 311.48 |
| 22 | 26.43 | 75 | 385.21 |
| 23 | 28.11 | 80 | 473.3 |
| 24 | 29.82 | 85 | 577.69 |
| 25 | 31.66 | 90 | 700.73 |
| 26 | 33.6 | 95 | 844.98 |
| 27 | 35.64 | 100 | 1013.17 |
| 28 | 37.78 | 110 | 1433.61 |
| 29 | 40.04 | 120 | 1988.84 |
| 30 | 42.42 | 130 | 2709.58 |
Partial oxygen pressure then equates to:
| 20.95 |
| 100 |
| ppO2 | Partial Pressure O2 (mbar) |
| BP | Barometric Pressure (mbar) |
| WVP | Water Vapour Pressure (mbar) |
Example 2 below describes the effect of humidity reducing the partial oxygen pressure and therefore the volumetric content of oxygen.
Example 2:
On a typical day, the following information is recorded from a calibrated weather station:
| Temperature | 22°C |
| Humidity | 32% |
| Barometric Pressure | 986mbar |
Using the Water Vapour Pressure look up table above, WVPmax = 26.43mbar.
| 32 |
| 100 |
Partial oxygen pressure then equates to:
| 20.95 |
| 100 |
As we now know the oxygen partial pressure and the total barometric pressure we can work out the volumetric content of oxygen.
| 204.8 |
| 986 |
Want to see more information like this?
Sign up to one of our Industry newsletters and you’ll receive our most-recent related news and insights all directly to your inbox!
Sign Up